Many sampling algorithms take as input random numbers in the [0..1) interval. On the other hand, Pseudo-Random Number Generators usually produce their output as (unsigned) integer 32-bit or 64-bit numbers.

It is trivial to turn an u:u32 integer into an f:[0..1] floating-point value, dividing u by 2^32-1. This is because u ranges in [0..2^32-1].

One might think that u/2^32 would produce a floating-point value lower than 1. But it does not, as evidenced by this loop:

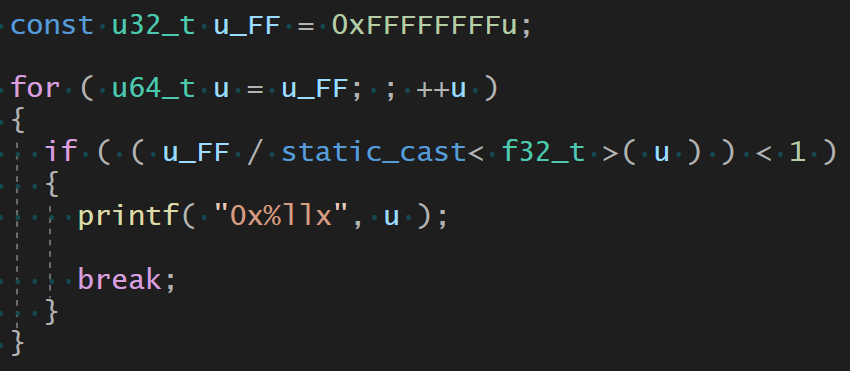
Better u32 to f32 conversion

The number printed out happens to be 0x100000101 which is 2^32+257.

( u / static_cast< f32_t >( 0x100000101ull ) ) is the f:[0..1) we were looking for.

( u / static_cast< f64_t >( 0x100000080ull ) ) does the same in double-precision.